Maximum Likelihood Estimation (MLE) is a statistical method used for estimating the parameters of a given statistical model. It is based on the principle of maximizing the likelihood function, ensuring that the observed data is most probable under the assumed statistical model.
The Concept of Likelihood
The likelihood of a statistical model is a function that measures the probability of observing the given data for different parameter values. For a set of parameters, ![]() , and given observations,
, and given observations, ![]() , the likelihood is defined as the probability of
, the likelihood is defined as the probability of ![]() given
given ![]() , denoted as
, denoted as ![]() . Mathematically, it is written as:
. Mathematically, it is written as:
(1) ![]()
Maximum Likelihood Estimation
MLE involves finding the parameter values that maximize the likelihood function. This process consists of the following steps:
- Define the likelihood function for the statistical model based on the probability distribution of the data.
- Convert the likelihood function to a log-likelihood function for computational ease:
(2) ![]()
- Differentiate the log-likelihood function with respect to the parameters. Set these derivatives equal to zero to find the maximum likelihood estimates (MLEs).
- Solve the resulting equations to obtain the parameter estimates.
Advantages and Limitations of MLE
Advantages
- Consistency: As the sample size increases, MLE tends to provide more accurate estimates.
- Efficiency: MLE estimates often have the smallest variance among all unbiased estimators.
- Invariance: The MLE of a function of parameters is the same function of the MLEs of those parameters.
Limitations
- Overfitting: MLE can overfit the model, especially in cases with small sample sizes or large number of parameters.
- Sensitivity to Model Specifications: MLE is highly sensitive to the assumed statistical model of the data.
- Complexity in Calculation: For complex models, the maximization of the likelihood function can be computationally challenging.
Example Problem and Solution
Problem Statement
Suppose we have a dataset ![]() , which represents samples drawn from a normal distribution. The task is to estimate the mean (
, which represents samples drawn from a normal distribution. The task is to estimate the mean (![]() ) of this distribution, assuming the variance (
) of this distribution, assuming the variance (![]() ) is known and equals 4 (i.e.,
) is known and equals 4 (i.e., ![]() ).
).
Solution
Given the likelihood function for a normal distribution, the task is to find the value of ![]() that maximizes this likelihood.
that maximizes this likelihood.
The likelihood function is:
(3) ![]()
For our dataset ![]() and
and ![]() , the log-likelihood function becomes:
, the log-likelihood function becomes:
(4) 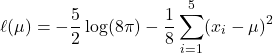
Differentiating ![]() with respect to
with respect to ![]() gives:
gives:
(5) 
Setting this derivative to zero for maximization:
(6) 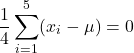
Solving for ![]() gives:
gives:
(7) 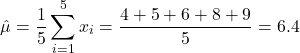
Thus, the MLE of the mean of this normally distributed population, given the known variance of 4, is 6.4.
Conclusion
MLE is a powerful and widely-used method in statistical inference, providing a framework for parameter estimation by maximizing the likelihood of observing the given data. While it has its advantages, such as consistency and efficiency, it also faces limitations like sensitivity to model specifications and complexity in calculations.

